Bedingte Wahrscheinlichkeit und Corona-Tests
GuG-Studierende des dritten Semesters befassten sich im Rahmen der Übung Ausgleichungsrechnung und Statistik I mit dem Prinzip der bedingten Wahrscheinlichkeit, welches sie auf das Themengebiet der Corona-Tests (PCR) anwendeten. Seien A und B zwei (nicht unmögliche) Ereignisse, so gilt nach dem Satz von Bayes für die Wahrscheinlichkeit, dass B eintritt unter der Voraussetzung, dass A eingetreten ist:
Für Corona-Tests oder andere medizinische Tests wird als Qualitätsmaß häufig die Größe der Sensitivität angegeben, seltener die sogenannte Spezifität. Bei der Spezifität handelt es sich um die Wahrscheinlichkeit, dass ein Test ein negatives Ergebnis (¯P) zeigt, vorausgesetzt der Patient ist gesund (¯K). Die Sensitivität gibt die Wahrscheinlichkeit dafür an, dass der Test anschlägt (P), vorausgesetzt der Patient ist krank (K). Diese Größen können aus klinischen Studien abgeleitet werden. In Formelschreibweise handelt es sich also um
| Spezifität | Sensitivität |
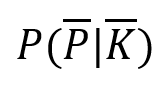 |
|
In der Anwendung der Corona-Tests erhält man allerdings ein Testergebnis (Voraussetzung) und leitet aus diesem den Gesundheitszustand ab. Es handelt sich also in Formelschreibweise um die Zustände
| Voraussetzung: Test ist negativ | Voraussetzung: Test ist positiv |
|
oder nicht krank |
oder nicht krank (falsch positiv) |
Die Studierenden untersuchten nun unter Anwendung des Satzes von Bayes die Wahrscheinlichkeit von Falsch-Positiv- und Falsch-Negativ-Ergebnissen in Abhängigkeit der sogenannten Prävalenz P(K) – dem Vorkommen der Krankheit in der getesteten Bevölkerung bzw. in anderer Nomenklatur der A-Priori-Wahrscheinlichkeit dafür, dass ein Mensch in der Gruppe der getesteten erkrankt ist.
Für zwei exemplarische Werte der Spezifität von 0.95 und Sensitivität von 0.98 zeigt Abbildung 1 das Ergebnis der Studierenden Ramon Butzer, Jan Heintz und Chuang Yu.
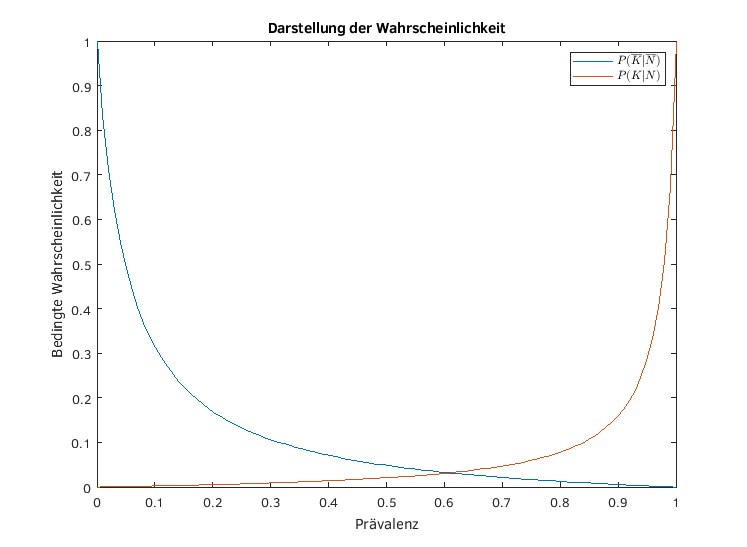
Abb. 1: Darstellung der bedingten Wahrscheinlichkeiten der fälschlicherweise positiven Tests (blau) und fälschlicherweise negativen Tests (orange). Hier wurde die Notation N anstelle von ¯P gewählt.
Die blaue Linie zeigt die Falsch-Positiv Wahrscheinlichkeit, die orangefarbene Linie die Falsch-Negativ-Wahrscheinlichkeit jeweils in Abhängigkeit der Prävalenz.
Die Studierenden stellten fest:
|
In den Grenzwerten ist das Verhalten klar.
|
Auf den ersten Blick ist das doch nicht ganz intuitiv. |
|
Die Werte, die wir für Sensitivität und Spezifität genutzt haben, sind nicht passend.
|
Achtung vor ausgelassenen Informationen und polemischer Rhetorik! |

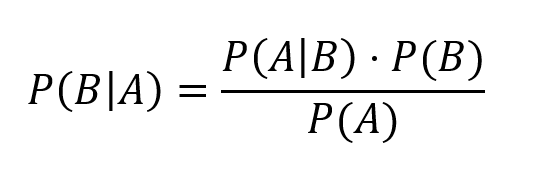
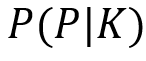
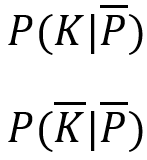 Person ist krank (falsch negativ)
Person ist krank (falsch negativ)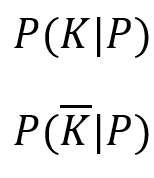 Person ist krank
Person ist krank